Hybrid Deep GP models: combining GP and Neural Network layers

In this notebook we show how to combine gpflux.layers.GPLayer layers with plain Keras neural network layers. This allows one to build hybrid deep GP models. Compared to the other tutorials, we are also going to use Keras’s Sequential model to build our hierarchical model and use a gpflux.losses.LikelihoodLoss instead of a gpflux.layers.LikelihoodLayer.

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

import gpflow
import gpflux

from gpflow.config import default_float
from gpflow.keras import tf_keras

2024-06-20 12:03:19.766046: I tensorflow/tsl/cuda/cudart_stub.cc:28] Could not find cuda drivers on your machine, GPU will not be used.
2024-06-20 12:03:19.796569: I tensorflow/tsl/cuda/cudart_stub.cc:28] Could not find cuda drivers on your machine, GPU will not be used.
2024-06-20 12:03:19.797555: I tensorflow/core/platform/cpu_feature_guard.cc:182] This TensorFlow binary is optimized to use available CPU instructions in performance-critical operations.
To enable the following instructions: AVX2 FMA, in other operations, rebuild TensorFlow with the appropriate compiler flags.
2024-06-20 12:03:20.537409: W tensorflow/compiler/tf2tensorrt/utils/py_utils.cc:38] TF-TRT Warning: Could not find TensorRT

Load Snelson dataset

We use a simple one-dimensional dataset to allow for easy plotting. To help training we normalize the input features.

d = np.load("../../tests/snelson1d.npz")
X, Y = data = d["X"], d["Y"]
X = (X - X.mean()) / X.std()
num_data, input_dim = X.shape

Initialize the GP Layer

As per usual we create a one-dimensional gpflux.layers.GPLayer with a simple SquaredExponential kernel and InducingPoints inducing variable:

num_data = len(X)
num_inducing = 10
output_dim = Y.shape[1]

kernel = gpflow.kernels.SquaredExponential()
inducing_variable = gpflow.inducing_variables.InducingPoints(
    np.linspace(X.min(), X.max(), num_inducing).reshape(-1, 1)
)
gp_layer = gpflux.layers.GPLayer(
    kernel, inducing_variable, num_data=num_data, num_latent_gps=output_dim
)

/home/runner/work/GPflux/GPflux/gpflux/layers/gp_layer.py:175: UserWarning: Beware, no mean function was specified in the construction of the `GPLayer` so the default `gpflow.mean_functions.Identity` is being used. This mean function will only work if the input dimensionality matches the number of latent Gaussian processes in the layer.
  warnings.warn(
/home/runner/work/GPflux/GPflux/gpflux/layers/gp_layer.py:198: UserWarning: Could not verify the compatibility of the `kernel`, `inducing_variable` and `mean_function`. We advise using `gpflux.helpers.construct_*` to create compatible kernels and inducing variables. As `num_latent_gps=1` has been specified explicitly, this will be used to create the `q_mu` and `q_sqrt` parameters.
  warnings.warn(

Sequential Keras model with GP and Neural net layers

We construct a model that consists of three tf.keras.layers.Dense layers and a GP. The first two Dense layers are configured to have 100 units and use a ReLU non-linearity. The last neural network layers reduces the dimension to one and does not utilise a non-linearity. We can interpret these three neural network layers as performing non-linear feature warping. The final layer in the model is the GP we defined above.

likelihood = gpflow.likelihoods.Gaussian(0.1)

# So that Keras can track the likelihood variance, we need to provide the likelihood as part of a "dummy" layer:
likelihood_container = gpflux.layers.TrackableLayer()
likelihood_container.likelihood = likelihood

model = tf_keras.Sequential(
    [
        tf_keras.layers.Dense(100, activation="relu"),
        tf_keras.layers.Dense(100, activation="relu"),
        tf_keras.layers.Dense(1, activation="linear"),
        gp_layer,
        likelihood_container,  # no-op, for discovering trainable likelihood parameters
    ]
)
loss = gpflux.losses.LikelihoodLoss(likelihood)

/tmp/ipykernel_2997/2725319331.py:4: DeprecationWarning: Call to deprecated class TrackableLayer. (GPflux's `TrackableLayer` was prior to TF2.5 used to collect GPflow variables in subclassed layers. As of TF 2.5, `tf.Module` supports this natively and there is no need for `TrackableLayer` anymore. It will be removed in GPflux version `1.0.0`.)
  likelihood_container = gpflux.layers.TrackableLayer()

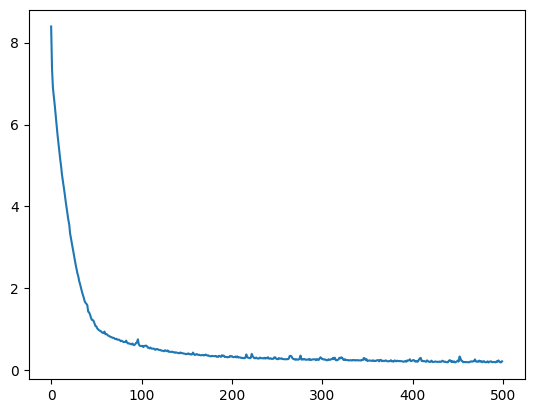
We compile our model by specifying the loss and the optimizer to use. After this is done, we fit the data and plot the trajectory of the loss:

model.compile(loss=loss, optimizer="adam")
hist = model.fit(X, Y, epochs=500, verbose=0)
plt.plot(hist.history["loss"])

[<matplotlib.lines.Line2D at 0x7f54be7cdd00>]

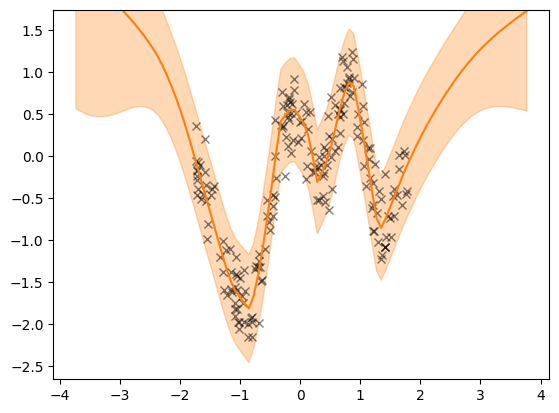
We can now inspect the final model by plotting its predictions. Note that model(X_test) now returns the output of the final GPLayer and not a LikelihoodLayer. The output of a GPLayer is a TFP distribution with a mean() and variance().

def plot(model, X, Y, ax=None):
    if ax is None:
        fig, ax = plt.subplots()

    x_margin = 2.0
    N_test = 100
    X_test = np.linspace(X.min() - x_margin, X.max() + x_margin, N_test).reshape(-1, 1)
    f_distribution = model(X_test)

    mean = f_distribution.mean().numpy().squeeze()
    var = f_distribution.variance().numpy().squeeze() + model.layers[-1].likelihood.variance.numpy()
    X_test = X_test.squeeze()
    lower = mean - 2 * np.sqrt(var)
    upper = mean + 2 * np.sqrt(var)

    ax.set_ylim(Y.min() - 0.5, Y.max() + 0.5)
    ax.plot(X, Y, "kx", alpha=0.5)
    ax.plot(X_test, mean, "C1")

    ax.fill_between(X_test, lower, upper, color="C1", alpha=0.3)


plot(model, X, Y)

gpflow.utilities.print_summary(model, fmt="notebook")

name	class	transform	prior	trainable	shape	dtype	value
Sequential._self_tracked_trackables[1]._trainable_weights[0] Sequential._self_tracked_trackables[1].kernel	UnliftedInitializerVariable			True	(1, 100)	float32	[[0.19218217, -0.13338092, 0.0139208...
Sequential._self_tracked_trackables[1]._trainable_weights[1] Sequential._self_tracked_trackables[1].bias	UnliftedInitializerVariable			True	(100,)	float32	[-0.03010563, 0.01673081, 0.12579736...
Sequential._self_tracked_trackables[2]._trainable_weights[0] Sequential._self_tracked_trackables[2].kernel	UnliftedInitializerVariable			True	(100, 100)	float32	[[-0.13662289, -0.77549344, -0.7601752...
Sequential._self_tracked_trackables[2]._trainable_weights[1] Sequential._self_tracked_trackables[2].bias	UnliftedInitializerVariable			True	(100,)	float32	[0.12514251, 0.04522482, 0.08523437...
Sequential._self_tracked_trackables[3]._trainable_weights[0] Sequential._self_tracked_trackables[3].kernel	UnliftedInitializerVariable			True	(100, 1)	float32	[[0.5161063...
Sequential._self_tracked_trackables[3]._trainable_weights[1] Sequential._self_tracked_trackables[3].bias	UnliftedInitializerVariable			True	(1,)	float32	[-0.10624776]
Sequential._self_tracked_trackables[4]._trainable_weights[0]	ResourceVariable			True	(10, 1)	float64	[[-0.66325536...
Sequential._self_tracked_trackables[4]._trainable_weights[1]	ResourceVariable			True	(1, 55)	float64	[[0.89333245, 0.28838355, -0.25918222...
Sequential._self_tracked_trackables[4]._metrics[0]._non_trainable_weights[0] Sequential._self_tracked_trackables[4]._metrics[0].total	UnliftedInitializerVariable			False	()	float64	0.26320830053171324
Sequential._self_tracked_trackables[4]._metrics[0]._non_trainable_weights[1] Sequential._self_tracked_trackables[4]._metrics[0].count	UnliftedInitializerVariable			False	()	float64	8.0
Sequential._self_tracked_trackables[4]._self_tracked_trackables[1].variance Sequential._self_tracked_trackables[4].kernel.variance	Parameter	Softplus		True	()	float64	0.8161940601106827
Sequential._self_tracked_trackables[4]._self_tracked_trackables[1].lengthscales Sequential._self_tracked_trackables[4].kernel.lengthscales	Parameter	Softplus		True	()	float64	0.9339522156896336
Sequential._self_tracked_trackables[4]._self_tracked_trackables[2].Z Sequential._self_tracked_trackables[4].inducing_variable.Z	Parameter	Identity		True	(10, 1)	float64	[[-1.53848...
Sequential._self_tracked_trackables[4]._self_tracked_trackables[4] Sequential._self_tracked_trackables[4].q_mu	Parameter	Identity		True	(10, 1)	float64	[[-0.66325536...
Sequential._self_tracked_trackables[4]._self_tracked_trackables[5] Sequential._self_tracked_trackables[4].q_sqrt	Parameter	FillTriangular		True	(1, 10, 10)	float64	[[[0.33280035, 0., 0....
Sequential._self_tracked_trackables[5]._self_tracked_trackables[0].variance Sequential._self_tracked_trackables[5].likelihood.variance Sequential._output_layers[0]._self_tracked_trackables[0].variance Sequential._output_layers[0].likelihood.variance Sequential._output_coordinates[0][0]._self_tracked_trackables[0].variance Sequential._output_coordinates[0][0].likelihood.variance	Parameter	Softplus + Shift		True	()	float64	0.09509551770450522