Welcome to GPflux#

GPflux is a research toolbox dedicated to Deep Gaussian processes (DGP) [DL13], the hierarchical extension of Gaussian processes (GP) created by feeding the output of one GP into the next.

GPflux uses the mathematical building blocks from GPflow [vdWDJ+20] and marries these with the powerful layered deep learning API provided by Keras. This combination leads to a framework that can be used for:

  • researching (deep) Gaussian process models (e.g., [DSHD18, SD17, SDHD19]), and

  • building, training, evaluating and deploying (deep) Gaussian processes in a modern way, making use of the tools developed by the deep learning community.

Getting started#

We have provided multiple Tutorials showing the basic functionality of the toolbox, and have a comprehensive API Reference.

As a quick teaser, here’s a snippet from the intro notebook that demonstrates how a two-layer DGP is built and trained with GPflux for a simple one-dimensional dataset:

# Layer 1
Z = np.linspace(X.min(), X.max(), X.shape[0] // 2).reshape(-1, 1)
kernel1 = gpflow.kernels.SquaredExponential()
inducing_variable1 = gpflow.inducing_variables.InducingPoints(Z.copy())
gp_layer1 = gpflux.layers.GPLayer(
   kernel1, inducing_variable1, num_data=X.shape[0], num_latent_gps=X.shape[1]
)

# Layer 2
kernel2 = gpflow.kernels.SquaredExponential()
inducing_variable2 = gpflow.inducing_variables.InducingPoints(Z.copy())
gp_layer2 = gpflux.layers.GPLayer(
   kernel2,
   inducing_variable2,
   num_data=X.shape[0],
   num_latent_gps=X.shape[1],
   mean_function=gpflow.mean_functions.Zero(),
)

# Initialise likelihood and build model
likelihood_layer = gpflux.layers.LikelihoodLayer(gpflow.likelihoods.Gaussian(0.1))
two_layer_dgp = gpflux.models.DeepGP([gp_layer1, gp_layer2], likelihood_layer)

# Compile and fit
model = two_layer_dgp.as_training_model()
model.compile(gpflow.keras.tf_keras.optimizers.Adam(0.01))
history = model.fit({"inputs": X, "targets": Y}, epochs=int(1e3), verbose=0)

The model described above produces the fit shown in Fig 1. For comparison, in Fig. 2 we show the fit on the same dataset by a vanilla single-layer GP model.

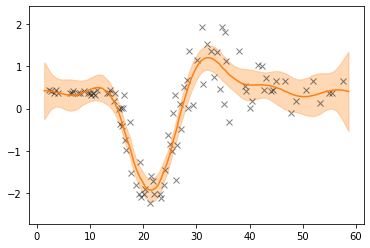
Fit on the Motorcycle dataset of a two-layer deep Gaussian process.

Fig 1. Two-Layer Deep GP#
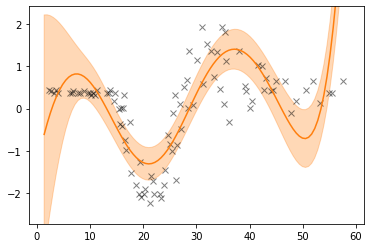
Fit on the Motorcycle dataset of a single-layer Gaussian process.

Fig 2. Single-Layer GP#

Installation#

Latest release from PyPI#

To install GPflux using the latest release from PyPI, run

$ pip install gpflux

The library supports Python 3.7 onwards, and uses semantic versioning.

Latest development release from GitHub#

In a check-out of the develop branch of the GPflux GitHub repository, run

$ pip install -e .

Join the community#

GPflux is an open source project. We welcome contributions. To submit a pull request, file a bug report, or make a feature request, see the contribution guidelines.

We have a public Slack workspace. Please use this invite link if you’d like to join, whether to ask short informal questions or to be involved in the discussion and future development of GPflux.

Bibliography#

[DL13]

Andreas Damianou and Neil D Lawrence. Deep Gaussian processes. In Artificial intelligence and statistics. 2013.

[DSHD18]

Vincent Dutordoir, Hugh Salimbeni, James Hensman, and Marc Deisenroth. Gaussian process conditional density estimation. In Advances in Neural Information Processing Systems. 2018.

[LDJD20]

Felix Leibfried, Vincent Dutordoir, ST John, and Nicolas Durrande. A tutorial on sparse gaussian processes and variational inference. arXiv preprint arXiv:2012.13962, 2020.

[RR07]

Ali Rahimi and Benjamin Recht. Random features for large-scale kernel machines. In Advances in Neural Information Processing Systems. 2007.

[RW06]

CE. Rasmussen and CKI. Williams. Gaussian Processes for Machine Learning. Adaptive Computation and Machine Learning. MIT Press, Cambridge, MA, USA, January 2006.

[SD17]

Hugh Salimbeni and Marc Deisenroth. Doubly stochastic variational inference for deep Gaussian processes. In Advances in Neural Information Processing Systems. 2017.

[SDHD19]

Hugh Salimbeni, Vincent Dutordoir, James Hensman, and Marc Deisenroth. Deep Gaussian processes with importance-weighted variational inference. In International Conference on Machine Learning. 2019.

[SS15]

Dougal J Sutherland and Jeff Schneider. On the error of random Fourier features. In Proceedings of the Thirty-First Conference on Uncertainty in Artificial Intelligence, 862–871. 2015.

[vdWDJ+20]

Mark van der Wilk, Vincent Dutordoir, ST John, Artem Artemev, Vincent Adam, and James Hensman. A framework for interdomain and multioutput Gaussian processes. arXiv preprint arXiv:2003.01115, 2020.

[WBT+20]

James Wilson, Viacheslav Borovitskiy, Alexander Terenin, Peter Mostowsky, and Marc Deisenroth. Efficiently sampling functions from Gaussian process posteriors. In International Conference on Machine Learning. 2020.

[YSC+16]

Felix Xinnan X Yu, Ananda Theertha Suresh, Krzysztof M Choromanski, Daniel N Holtmann-Rice, and Sanjiv Kumar. Orthogonal random features. Advances in Neural Information Processing Systems, 29:1975–1983, 2016.