Using deep Gaussian processes with GPflux for Bayesian optimization.#
[1]:
import numpy as np
import tensorflow as tf
np.random.seed(1794)
tf.random.set_seed(1794)
Describe the problem#
In this notebook, we show how to use deep Gaussian processes (DGPs) for Bayesian optimization using Trieste and GPflux. DGPs may be better for modeling non-stationary objective functions than standard GP surrogates, as discussed in [DKvdH+17, HBB+19].
In this example, we look to find the minimum value of the two- and five-dimensional Michalewicz functions over the hypercubes \([0, pi]^2\)/\([0, pi]^5\). We compare a two-layer DGP model with GPR, using Thompson sampling for both.
The Michalewicz functions are highly non-stationary and have a global minimum that’s hard to find, so DGPs might be more suitable than standard GPs, which may struggle because they typically have stationary kernels that cannot easily model non-stationarities.
[2]:
import gpflow
from trieste.objectives import Michalewicz2, Michalewicz5
from trieste.objectives.utils import mk_observer
from trieste.experimental.plotting import plot_function_plotly
function = Michalewicz2.objective
F_MINIMIZER = Michalewicz2.minimum
search_space = Michalewicz2.search_space
fig = plot_function_plotly(function, search_space.lower, search_space.upper)
fig.update_layout(height=800, width=800)
fig.show()
/opt/hostedtoolcache/Python/3.7.15/x64/lib/python3.7/site-packages/gpflow/experimental/utils.py:43: UserWarning: You're calling gpflow.experimental.check_shapes.decorator.check_shapes which is considered *experimental*. Expect: breaking changes, poor documentation, and bugs.
f"You're calling {name} which is considered *experimental*."
/opt/hostedtoolcache/Python/3.7.15/x64/lib/python3.7/site-packages/gpflow/experimental/utils.py:43: UserWarning: You're calling gpflow.experimental.check_shapes.inheritance.inherit_check_shapes which is considered *experimental*. Expect: breaking changes, poor documentation, and bugs.
f"You're calling {name} which is considered *experimental*."
Sample the observer over the search space#
We set up the observer as usual, using Sobol sampling to sample the initial points.
[3]:
import trieste
observer = mk_observer(function)
num_initial_points = 20
num_steps = 20
initial_query_points = search_space.sample_sobol(num_initial_points)
initial_data = observer(initial_query_points)
Model the objective function#
The Bayesian optimization procedure estimates the next best points to query by using a probabilistic model of the objective. We’ll use a two layer deep Gaussian process (DGP), built using GPflux. We also compare to a (shallow) GP.
Since DGPs can be hard to build, Trieste provides some basic architectures: here we use the build_vanilla_deep_gp function which returns a GPflux model of DeepGP class. As with other models (e.g. GPflow), we cannot use it directly in Bayesian optimization routines, we need to pass it through an appropriate wrapper, DeepGaussianProcess wrapper in this case. Additionally, since the GPflux interface does not currently support copying DGP architectures, if we wish to have the Bayesian
optimizer track the model state, we need to pass in the DGP as a callable closure so that the architecture can be recreated when required (alternatively, we can set set_state=False on the optimize call).
A few other useful notes regarding building a DGP model: The DGP model requires us to specify the number of inducing points, as we don’t have the true posterior. To train the model we have to use a stochastic optimizer; Adam is used by default, but we can use other stochastic optimizers from TensorFlow. GPflux allows us to use the Keras fit method, which makes optimizing a lot easier - this method is used in the background for training the model.
[4]:
from functools import partial
from trieste.models.gpflux import DeepGaussianProcess, build_vanilla_deep_gp
def build_dgp_model(data, search_space):
dgp = partial(
build_vanilla_deep_gp,
data,
search_space,
2,
100,
likelihood_variance=1e-5,
trainable_likelihood=False,
)
return DeepGaussianProcess(dgp)
dgp_model = build_dgp_model(initial_data, search_space)
/opt/hostedtoolcache/Python/3.7.15/x64/lib/python3.7/site-packages/gpflow/experimental/utils.py:43: UserWarning:
You're calling gpflow.experimental.check_shapes.checker.ShapeChecker.__init__ which is considered *experimental*. Expect: breaking changes, poor documentation, and bugs.
WARNING:tensorflow:From /opt/hostedtoolcache/Python/3.7.15/x64/lib/python3.7/site-packages/tensorflow_probability/python/distributions/distribution.py:346: calling MultivariateNormalDiag.__init__ (from tensorflow_probability.python.distributions.mvn_diag) with scale_identity_multiplier is deprecated and will be removed after 2020-01-01.
Instructions for updating:
`scale_identity_multiplier` is deprecated; please combine it into `scale_diag` directly instead.
Run the optimization loop#
We can now run the Bayesian optimization loop by defining a BayesianOptimizer and calling its optimize method.
The optimizer uses an acquisition rule to choose where in the search space to try on each optimization step. We’ll start by using Thompson sampling.
We’ll run the optimizer for twenty steps. Note: this may take a while!
[5]:
from trieste.acquisition.rule import DiscreteThompsonSampling
bo = trieste.bayesian_optimizer.BayesianOptimizer(observer, search_space)
grid_size = 1000
acquisition_rule = DiscreteThompsonSampling(grid_size, 1)
dgp_result = bo.optimize(
num_steps,
initial_data,
dgp_model,
acquisition_rule=acquisition_rule,
)
dgp_dataset = dgp_result.try_get_final_dataset()
WARNING:tensorflow:5 out of the last 5 calls to <function dgp_feature_decomposition_trajectory.__call__ at 0x7f400e50b0e0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details.
WARNING:tensorflow:6 out of the last 6 calls to <function dgp_feature_decomposition_trajectory.__call__ at 0x7f400c99ef80> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details.
Optimization completed without errors
Explore the results#
We can now get the best point found by the optimizer. Note this isn’t necessarily the point that was last evaluated.
[6]:
dgp_query_points = dgp_dataset.query_points.numpy()
dgp_observations = dgp_dataset.observations.numpy()
dgp_arg_min_idx = tf.squeeze(tf.argmin(dgp_observations, axis=0))
print(f"query point: {dgp_query_points[dgp_arg_min_idx, :]}")
print(f"observation: {dgp_observations[dgp_arg_min_idx, :]}")
query point: [2.99989118 1.57520652]
observation: [-0.9992104]
We can visualise how the optimizer performed as a three-dimensional plot
[7]:
from trieste.experimental.plotting import add_bo_points_plotly
fig = plot_function_plotly(
function, search_space.lower, search_space.upper, alpha=0.5
)
fig.update_layout(height=800, width=800)
fig = add_bo_points_plotly(
x=dgp_query_points[:, 0],
y=dgp_query_points[:, 1],
z=dgp_observations[:, 0],
num_init=num_initial_points,
idx_best=dgp_arg_min_idx,
fig=fig,
)
fig.show()
We can visualise the model over the objective function by plotting the mean and 95% confidence intervals of its predictive distribution. Note that the DGP model is able to model the local structure of the true objective function.
[8]:
import matplotlib.pyplot as plt
from trieste.experimental.plotting import (
plot_regret,
plot_model_predictions_plotly,
)
fig = plot_model_predictions_plotly(
dgp_result.try_get_final_model(),
search_space.lower,
search_space.upper,
num_samples=100,
)
fig = add_bo_points_plotly(
x=dgp_query_points[:, 0],
y=dgp_query_points[:, 1],
z=dgp_observations[:, 0],
num_init=num_initial_points,
idx_best=dgp_arg_min_idx,
fig=fig,
figrow=1,
figcol=1,
)
fig.update_layout(height=800, width=800)
fig.show()
We now compare to a GP model with priors over the hyperparameters. We do not expect this to do as well because GP models cannot deal with non-stationary functions well.
[9]:
import gpflow
import tensorflow_probability as tfp
from trieste.models.gpflow import GaussianProcessRegression, build_gpr
gpflow_model = build_gpr(initial_data, search_space, likelihood_variance=1e-7)
gp_model = GaussianProcessRegression(gpflow_model)
bo = trieste.bayesian_optimizer.BayesianOptimizer(observer, search_space)
result = bo.optimize(
num_steps,
initial_data,
gp_model,
acquisition_rule=acquisition_rule,
)
gp_dataset = result.try_get_final_dataset()
gp_query_points = gp_dataset.query_points.numpy()
gp_observations = gp_dataset.observations.numpy()
gp_arg_min_idx = tf.squeeze(tf.argmin(gp_observations, axis=0))
print(f"query point: {gp_query_points[gp_arg_min_idx, :]}")
print(f"observation: {gp_observations[gp_arg_min_idx, :]}")
fig = plot_model_predictions_plotly(
result.try_get_final_model(),
search_space.lower,
search_space.upper,
)
fig = add_bo_points_plotly(
x=gp_query_points[:, 0],
y=gp_query_points[:, 1],
z=gp_observations[:, 0],
num_init=num_initial_points,
idx_best=gp_arg_min_idx,
fig=fig,
figrow=1,
figcol=1,
)
fig.update_layout(height=800, width=800)
fig.show()
Optimization completed without errors
query point: [2.19749989 1.58411493]
observation: [-1.79361068]
We see that the DGP model does a much better job at understanding the structure of the function. The standard Gaussian process model has a large signal variance and small lengthscales, which do not result in a good model of the true objective. On the other hand, the DGP model is at least able to infer the local structure around the observations.
We can also plot the regret curves of the two models side-by-side.
[10]:
gp_suboptimality = gp_observations - F_MINIMIZER.numpy()
dgp_suboptimality = dgp_observations - F_MINIMIZER.numpy()
_, ax = plt.subplots(1, 2)
plot_regret(
dgp_suboptimality,
ax[0],
num_init=num_initial_points,
idx_best=dgp_arg_min_idx,
)
plot_regret(
gp_suboptimality,
ax[1],
num_init=num_initial_points,
idx_best=gp_arg_min_idx,
)
ax[0].set_yscale("log")
ax[0].set_ylabel("Regret")
ax[0].set_ylim(0.5, 3)
ax[0].set_xlabel("# evaluations")
ax[0].set_title("DGP")
ax[1].set_title("GP")
ax[1].set_yscale("log")
ax[1].set_ylim(0.5, 3)
ax[1].set_xlabel("# evaluations")
[10]:
Text(0.5, 0, '# evaluations')
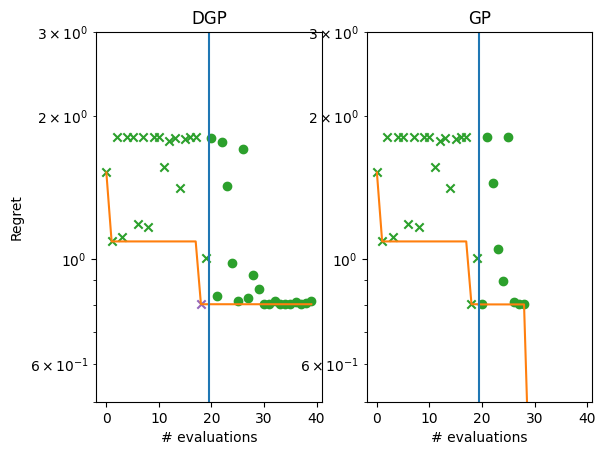
We might also expect that the DGP model will do better on higher dimensional data. We explore this by testing a higher-dimensional version of the Michalewicz dataset.
Set up the problem.
[11]:
function = Michalewicz5.objective
F_MINIMIZER = Michalewicz5.minimum
search_space = Michalewicz5.search_space
observer = mk_observer(function)
num_initial_points = 50
num_steps = 50
initial_query_points = search_space.sample_sobol(num_initial_points)
initial_data = observer(initial_query_points)
Build the DGP model and run the Bayes opt loop.
[12]:
dgp_model = build_dgp_model(initial_data, search_space)
bo = trieste.bayesian_optimizer.BayesianOptimizer(observer, search_space)
acquisition_rule = DiscreteThompsonSampling(grid_size, 1)
dgp_result = bo.optimize(
num_steps,
initial_data,
dgp_model,
acquisition_rule=acquisition_rule,
)
dgp_dataset = dgp_result.try_get_final_dataset()
dgp_query_points = dgp_dataset.query_points.numpy()
dgp_observations = dgp_dataset.observations.numpy()
dgp_arg_min_idx = tf.squeeze(tf.argmin(dgp_observations, axis=0))
print(f"query point: {dgp_query_points[dgp_arg_min_idx, :]}")
print(f"observation: {dgp_observations[dgp_arg_min_idx, :]}")
dgp_suboptimality = dgp_observations - F_MINIMIZER.numpy()
Optimization completed without errors
query point: [2.26823028 2.69381407 1.28974228 1.22838305 0.81679683]
observation: [-2.40526686]
Repeat the above for the GP model.
[13]:
gpflow_model = build_gpr(initial_data, search_space, likelihood_variance=1e-7)
gp_model = GaussianProcessRegression(gpflow_model)
bo = trieste.bayesian_optimizer.BayesianOptimizer(observer, search_space)
result = bo.optimize(
num_steps,
initial_data,
gp_model,
acquisition_rule=acquisition_rule,
)
gp_dataset = result.try_get_final_dataset()
gp_query_points = gp_dataset.query_points.numpy()
gp_observations = gp_dataset.observations.numpy()
gp_arg_min_idx = tf.squeeze(tf.argmin(gp_observations, axis=0))
print(f"query point: {gp_query_points[gp_arg_min_idx, :]}")
print(f"observation: {gp_observations[gp_arg_min_idx, :]}")
gp_suboptimality = gp_observations - F_MINIMIZER.numpy()
Optimization completed without errors
query point: [2.26823028 2.69381407 1.28974228 1.22838305 0.81679683]
observation: [-2.40526686]
Plot the regret.
[14]:
_, ax = plt.subplots(1, 2)
plot_regret(
dgp_suboptimality,
ax[0],
num_init=num_initial_points,
idx_best=dgp_arg_min_idx,
)
plot_regret(
gp_suboptimality,
ax[1],
num_init=num_initial_points,
idx_best=gp_arg_min_idx,
)
ax[0].set_yscale("log")
ax[0].set_ylabel("Regret")
ax[0].set_ylim(1.5, 6)
ax[0].set_xlabel("# evaluations")
ax[0].set_title("DGP")
ax[1].set_title("GP")
ax[1].set_yscale("log")
ax[1].set_ylim(1.5, 6)
ax[1].set_xlabel("# evaluations")
[14]:
Text(0.5, 0, '# evaluations')
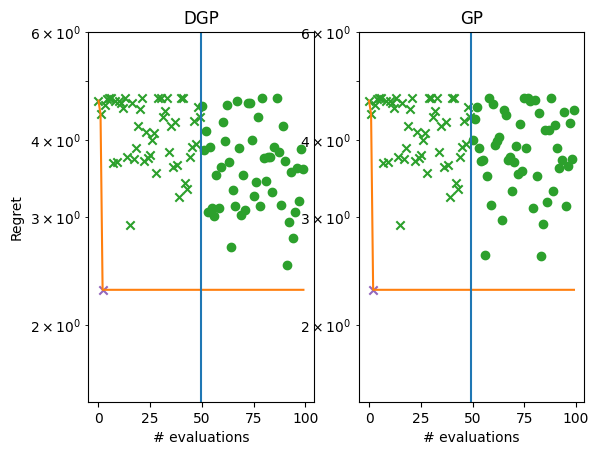
While still far from the optimum, it is considerably better than the GP.